Trigonometría

 Razones Trigonométricas

Seno

El seno del ángulo B es la razón entre el cateto opuesto al ángulo y la hipotenusa. Se denota por sen B.

 

 

Coseno

El coseno del ángulo B es la razón entre el cateto adyacente o contiguo al ángulo y la hipotenusa. Se denota por cos B.

 

Tangente

La tangente del ángulo B es la razón entre el cateto opuesto al ángulo y el cateto adyacente al ángulo. Se denota por tan B o tg B.

Cosecante

La cosecante del ángulo B es la razón inversa del seno de B.

Se denota por csc B o cosec B.

Secante

La secante del ángulo B es la razón inversa del coseno de B.

Se denota por sec B.

Cotangente

La cotangente del ángulo B es la razón inversa de la tangente de B.

Se denota por cot B o ctg B.

 

SOH-CAH-TOA: Una manera sencilla de recordar

SOH-CAH-TOA es un acrónimo que se usa para poder memorizar las definiciones de las razones trigonométricas más importantes: seno, coseno y tangente. La siguiente tabla explica su significado.

Para las otras razones trigonométricas, en vez de crear otro acrónimo, es más sencillo aprenderse el hecho de que la cosecante, secante y cotangente, son opuestos multiplicativos del seno, coseno y tangente, respectivamente. En la siguiente tabla se detalla.

Razones trigonométricas en una circunferencia

Se llama circunferencia gonio métrica o círculo unitario a aquella que tiene su centro en el origen de coordenadas y su radio es la unidad.
Si consideramos un triángulo rectángulo dentro del círculo con el radio forma la hipotenusa y uno de los catetos está sobre el eje X, obtendremos una figura como la siguiente.

Calculamos el seno y coseno del ángulo 

Concluímos que

El seno es la ordenada de P, es decir del punto que está sobre la circunferencia.

El coseno es la abscisa de P, es decir del punto que está sobre la circunferencia.

Otro dato que podemos deducir es que los valores de seno y coseno están entre 1 y -1.

-1 ≤ sen α ≤ 1

-1 ≤ cos α ≤ 1

Cabe destacar que la razón por la que se consideran las funciones trigonométricas en el círculo es para poder tomar ángulo más grandes. Por ejemplo, del un triángulo rectángulo no podría saber cuánto es , porque no puedo construir un triángulo rectángulo con un ángulo de 150°.

El círculo unitario me permite hacer ese cálculo. Lo que hago es:
1 Localizo el ángulo de 150° que se forma a partir del eje X en dirección opuesta a las manecillas del reloj.
2 Considero el punto sobre la circunferencia que se forma con el ángulo

• La ordenada de ese punto es el seno
• La abscisa es el coseno

Para las otras razones trigonométricas consideramos la siguiente figura

 

QOP y TOS son triángulos semejantes. Entonces,

QOP y T'OS′ son triángulos semejantes. 

Signo de las razones trigonométricas

En la circunferencia goniométrica los ejes de coordenadas delimitan cuatro cuadrantes que se numeran en sentido contrario a las agujas del reloj. Recordemos que si consideramos un ángulo  y tomamos el triángulo rectángulo dentro del círculo que se genera con dicho ángulo, el signo de el seno o coseno de este ángulo dependerá de en cuál cuadrante se ubique el triangulo.

 

 Tabla de razones trigonométricas

 

Relaciones pitagóricas entre las razones trigonométricas

Explicación:

Como el triángulo que se considera dentro del círculo es rectángulo se cumple que

En la imagen, los catetos (a y b) corresponden a los valores x y y, y la hipotenusa al radio, o sea , 1.
Como x es la abscisa y y la ordenada sabemos que estos valores corresponden al coseno y seno respectivamente.

Identidades trigonométricas

Las identidades trigonométricas son igualdades que involucran funciones trigonométricas. Estas identidades son siempre útiles para cuando necesitamos simplificar expresiones que tienen incluidas funciones trigonométricas, cualesquiera que sean los valores que se asignen a los ángulos para los cuales están definidas estas razones.Las identidades trigonométricas nos permiten plantear una misma expresión de diferentes formas. Para simplificar expresiones algebraicas, usamos la factorización, denominadores comunes, etc. Pero para simplificar expresiones trigonométricas utilizaremos estas técnicas en conjunto con las identidades trigonométricas.

Antes de comenzar a ver las diferentes identidades trigonométricas, debemos conocer algunos términos que usaremos bastante en trigonometría, que son las tres funciones más importantes dentro de esta. El coseno de un ángulo en un triángulo rectángulo se define como la razón entre el cateto adyacente y la hipotenusa:

Otra función que utilizaremos en trigonometría es “seno”. Definiremos seno como la razón entre el cateto opuesto y la hipotenusa en un triángulo rectángulo:

Mientras tanto la palabra tangente en matemática puede que tenga dos significados distintos. En geometría se utiliza el término de recta tangente, pero a nosotros en trigonometría nos interesa otro término que es el de tangente de un ángulo, el cual es la relación entre los catetos de un triángulo rectángulo , lo mimo que decir que es el valor numérico que resulta de dividir la longitud del cateto opuesto entre la del cateto adyacente al ángulo.

Las siguientes identidades se cumplen para cualquier ángulo en el cual el denominador no sea cero. Estas son identidades recíprocas:

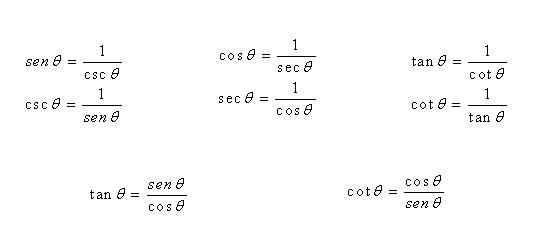
A partir de las relaciones pitagóricas es posible encontrar otras identidades y demostrar algunas identidades trigonométricas. Mediante estas relaciones si conocemos las medidas de los catetos de un triángulo rectángulo podemos calcular la medida de la hipotenusa (lado opuesto al ángulo recto) y si conocemos la medida de la hipotenusa y la de un cateto podemos calcular la medida del otro cateto. Entonces diremos que el teorema de Pitágoras es un teorema que se aplica únicamente a triángulos rectángulos, y nos sirve para obtener un lado o la hipotenusa de un triángulo, si es que se conocen los otros dos. Las identidades de relaciones pitagóricas son las siguientes:

De acuerdo al teorema de pitágoras :