Aritmética
Fracciones
¿Qué es una fracción?
Una fracción representa el número de partes que cogemos de una unidad que está dividida en partes iguales. Se representa por dos números separados por una línea de fracción.
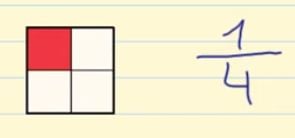
Términos de una fracción
Los términos de una fracción son el numerador y el denominador. El numerador es el número de partes que tenemos y el denominador es el número de partes en que hemos dividido la unidad.
Vamos a ver un ejemplo: Tenemos diferentes figuras y cada una de ellas la dividimos en diferentes partes iguales, que es el denominador. La parte coloreada es el numerador.
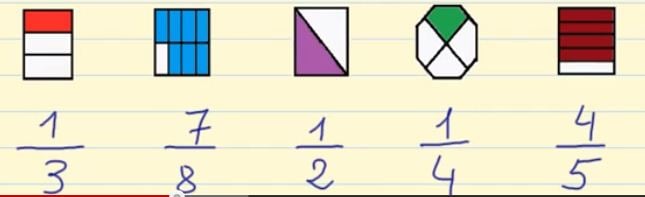
¿Cómo se leen las fracciones?
El numerador se lee con los números cardenales. 1 – un, 2 – dos, 3 – tres, …, 10 – diez, …, 24 – veinticuatro…
El denominador se lee con los números partitivos. 2 – medios, 3 – tercios, 4 – cuartos, 5 – quintos, 6 – sextos, 7 – séptimos, 8 – octavos, 9 – novenos, 10 – décimos. A partir del 11, el número se lee terminado en -avos: 11 – onceavos, 12 – doceavos, …
Tipos de fracciones
- Fracción propia: Cuando el numerador es menor que el denominador.
- Fracción impropia: Cuando el numerador es mayor que el denominador.
- Fracción unitaria: Cuando el numerador es igual que el denominador.
|
Partes de la división
Los términos o partes de la división son, el cociente y del resto, el dividendo y el divisor. Los términos dan lugar a las llamadas divisiones de una cifra (divisor con un solo dígito), divisiones de dos cifras (divisores de dos dígitos), divisiones con decimales en el dividendo y/o en el divisor, etc.

Veamos cada parte, una a una:
- Partes de la división:
- Dividendo: Es el número que hay que repartir. Para el ejemplo de la imagen, este número es el 125 que representan los caramelos.
- Divisor: Es el número entre el cual se divide el dividendo, es decir, las partes entre las que hay que repartir. Para nuestro ejemplo, este es el número 5 que representa a los cinco amigos entre los que hay que repartir los 125 caramelos.
- Cociente: Es el resultado de la división. En nuestro ejemplo, 25. Es decir, cada amigo toca a 25 caramelos.
- Resto: Es el número que sobra cuando se termina de hacer la división. Este número puede ser cero u otro número, pero siempre tiene que ser menor que el divisor. Representa la parte que no puede repartirse. En nuestro ejemplo, el resto es 0 porque hemos podido repartir todos los caramelos.
Divisiones de una cifra
Veamos ahora cómo se divide. Empezaremos haciendo divisiones de una sola cifra en el divisor. Seguiremos con el mismo ejemplo de antes, es decir, vamos a dividir 125 entre 5. Cuando comenzamos a estudiar las divisiones hay dos formas de resolverlas: con resta o sin ella. Vamos a ver el procedimiento de cada una de ellas.
Divisiones de una cifra con resta
Empezamos escribiendo la división.
![]()
Ahora tenemos que ver cuántas cifras tenemos que usar del dividendo para dividir por el divisor. La norma que hay que seguir siempre es que el número del dividendo que vamos a dividir debe ser igual o mayor al del divisor. Por ejemplo, en 125 no podemos empezar dividiendo 1 entre 5 porque 1 es menor que 5, así que cojo el siguiente número del dividendo. Ahora tengo el número 12 ¿es mayor que cinco? sí, así que ya puedo dividir.
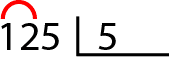
Ahora tenemos que calcular mentalmente qué número multiplicado por el divisor (5) se acerca más al dividendo (12) sin pasar a éste. Es decir, ¿qué número multiplicado por 2 se acerca más a 12 sin sobrepasarlo? Veamos, 5 x1 = 5, 5×2= 10, 5×3 =15 No podemos utilizar el 3 porque al multiplicarlo por 5 supera a 12, tampoco podemos utilizar el 1 porque al multiplicar por dos nos acercamos más a 12, puesto que 10 está mucho más cerca de 12 que 5. Así pues, ya sabemos que debemos multiplicar por 2. Anotamos 2 en el cociente y ponemos la multiplicación debajo del dividendo, en nuestro caso, 10.
Lo siguiente que debemos hacer es la resta de 12 menos 10 y anotar el resultado debajo. Para nuestro ejemplo, 2.
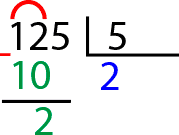
Debemos seguir con la división ya que nos falta parte del dividendo por hacer. Pasamos el siguiente número del dividendo (el 5) al lado del dos que teníamos y volvemos a hacernos la misma pregunta. Ahora sería, ¿qué número multiplicado por 5 se acerca más a 25? ¡qué fácil! en este caso es el 5, puesto que 5 x 5 =25. Anotamos el cinco en el cociente detrás del 2 y escribimos 25 debajo del 25 que ya teníamos.
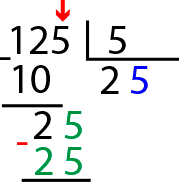
Ya solo nos queda hacer la resta final, 25 menos 25 es igual a 0, que es el resto de nuestra división. También podemos deducir con esto que 125 dividido entre 5 es igual 25.
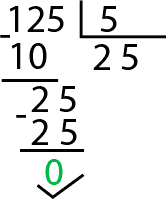
Divisiones de una cifra sin resta
Una vez se manejan bien las divisiones con resta ya estamos preparados para hacerlas sin ella. Este es un proceso mental que poco a poco iremos dominando para hacer así todas nuestras divisiones. Seguiremos con el mismo ejemplo para que puedas ver las diferencias. Lo primero, es escribir la división:
![]()
El siguiente paso también es igual. Cogemos el número del dividendo que sea mayor o igual al divisor, en nuestro caso 12. La pregunta es la misma también ¿qué número multiplicado por 5 se acerca más a 12? La respuesta es 2, así que escribimos un 2 en el cociente. Ahora viene la diferencia, restamos de cabeza sin anotarlo. Es decir 5 por 2 es igual a 10, 12 menos 10 es igual a 2, así que solo colocamos el 2 debajo del 12.
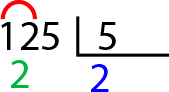
Ahora debemos seguir con el siguiente número del dividendo, así que anotamos el 5 al lado del 2.
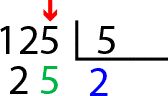
Ahora nos preguntamos qué número multiplicado por 5 se acerca o igual a 25. La respuesta es 5. Anotamos este 5 en el cociente detrás del 2 y restamos mentalmente 25 menos 25 que es igual a 0. Anotamos ese 0 en el resto. ¡Ya la hemos resuelto! 125 entre 5 es igual a 25.
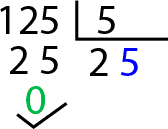
FRACCIONES COMPLEJAS O COMPUESTAS
Para simplificar fracciones complejas más complicadas debes tener en cuenta la jerarquía de las operaciones.
1º Signos de agrupación
2º Tomar potencias y raíces
3º Multiplicaciones y divisiones
4º Adiciones y sustracciones
Definición:
Se le llama fracción compleja o compuesta, a cualquier forma fraccionaria que tenga fracciones en el numerador o el denominador. Con frecuencia es necesario representar una fracción compleja en la forma de fracción simple
Se entiende por simplificación de una fracción compleja su transformación a una fracción simple, reducida en términos a sus términos más sencillos, que sea equivalente a ella. Pueden usarse dos métodos.
Uno: Consiste en transformar el numerador y denominador en fracciones simples (si es necesario) y luego proceder como en la división de fracciones.
Otro: Que generalmente es más sencillo, consiste en obtener una fracción simple multiplicando el numerador y el denominador originales por el menor denominador común de todas las fracciones.
Ejemplo 1 Dividiendo fracciones.
POTENCIACIÓN
Propiedades
La potenciación es la operación matemática que nos dice que un número llamado base, es multiplicado consigo mismo una cantidad de veces llamada exponente.

La expresión de arriba se lee “a elevado a la n”, y a su vez, equivale matemáticamente a la igualdad de abajo:

La notación tipográfica usada por convención para denotar la potenciación, es la siguiente: a^n. Por lo que, si necesitás buscar información sobre el tema, o la resolución de un ejercicio, es así como vas a encontrar los mejores resultados.
Es decir: 5² es 5 al cuadrado; y 5³ es 5 al cubo.
Matematicamente hablando, la potenciación es un tema de gran peso teórico, por lo que, adquirido éste conocimiento, la práctica isolada del tema es profundamente mecánica.
Concepto Importante
Existe un concepto evidente en la potenciación que es muy importante de recalcar: si a² = a * a, y basándonos en que toda multiplicación entre números positivos da como resultado, otro número positivo, podemos afirmar que:
- Todo número elevado a un exponente par, da como resultado otro número parEste axioma es muy usado en la matemática, y sobre todo, en su caso más simple: bases elevadas al cuadrado.Es más, esto es tan importante, que fue un factor que dio origen a la necesidad de los números complejos (pero eso no es un tema que nos compete ahora).
Dicho esto, pasamos a lo importante.
Propiedades
Siempre que estés cerca de las matemáticas, estarás relacionado con este tema, por lo que, aprendete bien las propiedades que te van a servir toda tu vida.
Producto de potencias de igual base: Como bien dice su nombre, si dos bases son iguales (el mismo número o variable), y son los factores de una multiplicación, ambas bases quedan en una sola y sus exponentes son sumados.

Para mí, junto con la que viene, es la más importante de todas, porque siempre está y porque a veces simplifica expresiones que parecen muy difíciles de trabajar.
Cociente de potencias de igual base: Acá las bases, que nuevamente deben ser iguales, son parte de una división. Como antes, nos quedamos con una sola base, y ahora sus exponentes se restan.

Nota: Tener en cuenta que a veces hay que aplicar las propiedades de derecha a izquierda, es decir, no estar solo atentos a que si tenemos un producto de potencias de igual base, hay que sumar los exponentes, sino que también, si tenemos una base elevada a una suma, estas habilitado a separar esa suma como exponente.
Nota²: Éstas propiedades toman fuerza cuando los exponentes(o las bases) no pueden ser trabajadas directamente, es decir, son variables de una ecuación o son números irracionales como (e o π). Ya que si son números normales, directamente se calcula el resultado de dicha expresión.
Por estos motivos, tener muy presente cuando se vean situaciones como las siguientes:


Nota: Como antes, tener en cuenta el camino inverso también. Muy útil para las ecuaciones de temática exponencial.

Potencia de exponente negativo: En estos casos, se obtiene el inverso de la expresión. Es decir, si tenemos una fracción, intercambiamos numerador por denominador (la damos vuelta); y si tenemos un entero, ese número se transforma en el denominador de una fracción cuyo numerador es 1. Luego, elevamos la fracción entera al exponente en cuestión.

Potencia de exponente cero: Cuando una base está elevada a 0, el resultado siempre es 1.

Distributividad de la potencia: La potencia es distributiva solo con respecto a la multiplicación y la división. No así respecto a las sumas y resta, lo que es un error muy común y muy grave.

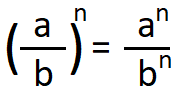
En otra ocasión veremos qué pasa cuando los números a y b se relacionan mediante una operación suma o resta.
Estas fueron las propiedades de la potenciación, recuerden tenerlas siempre presente, porque aunque no parezca, serán necesarias en cualquier momento que dependa de resoluciones de nivel aritmético.
RADICACIÓN
Propiedades
Racionalización
La racionalización consiste en eliminar los radicales del denominador.
Por ejemplo:
Hay tres tipos de racionalización:
Tipo 1:
Tipo 2:
LOGARITMOS
Definición de logaritmo
Exponente al que hay que elevar un número, llamado base, para obtener otro número determinado. Un logaritmo busca el exponente  de una base
de una base  que se ha empleado para llegar a un determinado resultado
que se ha empleado para llegar a un determinado resultado  .
.
Ejemplo:
Si tengo de base  y como resultado
y como resultado  , ¿a qué exponente se debe elevar el
, ¿a qué exponente se debe elevar el  para que nos dé como resultado
para que nos dé como resultado  ? Como te darás cuenta el valor del exponente que se utilizó para llegar al resultado
? Como te darás cuenta el valor del exponente que se utilizó para llegar al resultado  con la base
con la base  es
es 
donde  es la base,
es la base,  el resultado y
el resultado y  el exponente buscado. Hay que recalcar que se deben cumplir las condiciones de que la base sea positiva
el exponente buscado. Hay que recalcar que se deben cumplir las condiciones de que la base sea positiva  y distinta a uno .
y distinta a uno .








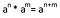
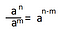

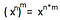
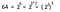
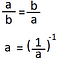
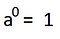

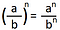




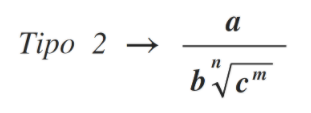

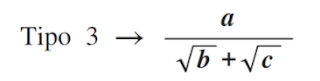

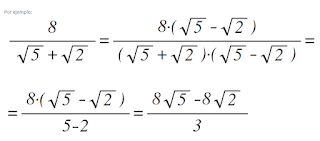

Comentarios
Publicar un comentario